数学建模

目录¶

0.0 数学建模之概念
0.1 作业与考试
0.2 数学基础与数学软件
1.1 秘密共享

数学建模之概念¶

在实际情境中从数学的角度发现问题，提出问题，分析问题，建立模型，确定参数，计算求解，检验结果，改进模型

作业与考试¶

巩固性作业
研究性作业
课程论文（小组）
期末开卷考试
微积分、线代、概率论等等建模（大部分到建模为止）
优化部分（动态规划，组合优化，线性规划，博弈论）

数学基础与数学软件¶

数学基础¶

微积分
线代
概统：随机事件，不确定的问题
微分方程
数论、代数、几何

微分方程¶

增长、扩散、竞争
偏微分方程模型（变分法，泛函分析）
简单控制问题

运筹学¶

连续优化
离散优化、图论
博弈、决策

数值计算、反问题（e.g方程求根、微分方程数值解、有限元）¶

随机数学模型¶

随机过程
排队论、库存论

数据分析、处理（数理统计、机器学习、数据挖掘、可视化）¶

社会科学中的数学方法（多属性决策）¶

计算机应用¶

启发式算法
模拟与仿真

程序设计语言（C，Python）¶

综合性数学软件（Matlab,Mathematica,Maple）¶

专业性数学软件（R,LINGO,CPLEX,Gurobi,COPT）¶

秘密共享（复记本节）¶

疑问：一把只有插入三把钥匙才能开的锁？
规则：

锁与钥匙：¶

安全门上至少要有 $\tbinom{2n+1}{2n}$ 把锁
- 任一"少数团体"至少有一把锁打不开

门限机制：¶

在n人之间共享秘密，其中任意 $t<n$ 人可以得到秘密，任意 $t-1$ 人不可以的得到秘密

Samir门限机制 $(r,n)$ ¶

一保险柜的开启密码为整数，规定当且仅当相关的个人中有个或以上在场方可开启

本质：线性方程组求解（范德蒙德行列式）

取同余的原因：更便于伪装（线代的定理在同余条件下亦成立）

中国剩余定理¶

同余的逆：若存在 $c是的a \cdot c = 1(mod\quad m),则称a模c可逆，记为a^-1(mod m)$

一次同余方程： $ax \equiv b$ ,有解的充要条件为 $(a,m)|b$ ,当 $(a,m) = 1$ 时，方程的解为 $a^{-1}b$

求解方法：待记

中国剩余定理： $一次同余方程组x \equiv a_j (mod\ m_j), i<j<k 的非负整数解是唯一的$

Asmuth-Bloom门限机制¶

参考链接：基于中国剩余定理的秘密共享

PageRank（复看）¶

建模的过程、建模与求解的统一

排序机制——网页重要度的原则与假设¶

网页通过超链接连接，网页重要程度由网络间的链接关系决定

某网页重要，是因为有重要的网页链接到它
对任一网页A，确定一数值，作为其重要度
链接到A的所有网页对A的重要度有贡献，贡献值与其重要度有关
传递性：链接到A的网页B，其重要度也会对A有贡献
某网页对其他网页重要度贡献之和等于他的重要度
等效性：网页对其连接的网页的重要度贡献相同
叠加性：网页的重要度等于其他网页对其的重要度贡献之和
无关性：网页链接到其他网页的数量不影响其重要度

网页重要度¶

网络链接图
1. 顶点：网页 $v_1,v_2\dots v_n$
2. 弧：网页间的链接
3. 出度：网页的出链数量
网页重要度
- 若链接到网页 $v_i$ 的网页有 $v_{j1},v_{j2},\dots v_{jn}$ ，则 $v_i$ 的重要度为： $x_j = \sum{_i} \frac{x_{ji}}{q_{ji}}=\sum \limits _{j=1}^n p_{ij}x_j$
- 矩阵表示
- 令 $p_{ij} = \frac{1}{q_j}$ （若有链接自 $v_j$ 向 $v_i$ ）,否则 $p_{ij} = 0$ （一个网页的贡献排成一列）
- 即矩阵 $P = (p_{ij})_{n \times n}$ 为链接矩阵，X为网页重要度向量
- X为线性方程组X=PX的解
  - 有解性的证明：矩阵I-P的每一列之和为0，故可得每一行线性相关，故有解
随机矩阵
- 特点：各行（列）元素之和均为1的非负方阵
- 性质：
- 模最大的特征值为1
不链接的网页（悬挂网页）的处理
- 将对应列中所有元素改为 $\frac{1}{n}$
- 看作原始矩阵加上修正矩阵： $\bar{P}=P+\frac{1}{n}ed^T$
特征值的特征向量唯一的修正（复记）
- 将 $\bar{P}$ 修改为 $\bar{\bar{P}} = \alpha \bar{P}+(1-\alpha)ee^T$
- 称
- 证明：

PageRank的数学基础¶

Parron-Frobenius定理：
- 不可约矩阵
- 置换矩阵：若干个初等对换矩阵的乘积
  - 置换矩阵每行每列都恰有一个元素为1，其余元素为0
- 若存在置换矩阵Q，使得
- 不可约矩阵与有向图
- 若对有向图中任意有序顶点对 $v_i,v_j$ （ij可相等），存在一条从 $v_i$ 到 $v_j$ 的有向路（无需双向），则称有向图是强联通的
- 若A为非负不可约矩阵，则

PageRank的计算实现¶

幂法：计算矩阵模最大特征值及其对应特征向量
1. 任取初始向量 $x^{0},x^{0}>0且e^Tx^{0}=1$ （即 $x^0$ 的各项之和为1）
2. 计算 $x^{k}=Px^{k-1}，即x^{k}=P^{k}x^{0}$ （迭代后的各项之和仍为1）
  
  对于链接矩阵 $\bar{\bar{P}}$ 来说，先把它拆分（根据之前的关系），再进行幂法迭代，最后再乘上 $\frac{1}{n}$ ，以简化计算

随机浏览模型¶

假设：用户在任一网页上有 $\alpha$ 的概率继续浏览当前网页，有 $1-\alpha$ 的概率随机跳转到其他网页

经过Page的调查， $\alpha$ 的取值约为 $\frac{5}{6}$ ，近似为0.85
从任一网页开始，充分长时间后，访问各网页的概率即为网页重要度
极限概率：即事件 $\{ X_m = j \}$ 为时刻m访问网页j，则 $P\{X_m = i\ |X_{m-1}=j\}=p_{ij}$
复记

马尔科夫过程¶

在已知目前状态条件下，未来演变不依赖于其以往的演变

数论及组合数学（复记）¶

安全状态与不安全状态¶

若无论对方如何去均不会获胜，则称为安全状态（对己方）
若存在一种方式，对方可以获胜，则称为不安全状态（对己方）
若无论对方如何取，己方下一次取法均能使其进入安全状态，则称为安全状态（对己方）
若对方至少存在一种取法，己方下一次取无法变为一个安全状态的状态也是不安全的

NIM游戏与二进制¶

二进制与位和
- 1

随机模型¶

疾病监测¶

灵敏度：患者被检测为阳性的概率
特异度：健康人被检测为阴性的概率

Monty Hall问题¶

数学期望¶

期望：期望的和等于和的期望
几何分布的期望： $\frac{1}{p}$

赌徒破产问题¶

面试问题¶

动态规划¶

差分方程¶

种群增长模型¶

离散单种群模型¶

1.假设¶

只由一个世代组成，相继世代之间没有重叠
第n代个体数量满足 $x_{n+1} = f(x_n)$

2.增长模型¶

离散指数增长模型
- $x_{n+1} = rx_n$
- $x_n = x_0\cdot r^n$

混沌¶

Li-Yorke定理：若映射 $f$ 有一个3周期点，那么 $f$ 是混沌的

连续单种群模型¶

生物数学模型¶

传染病--SIR模型¶

现阶段大多数基于SIR模型

1.模型假设¶

人口总数为N，且总是保持不变
人口分为三类
- 易感者S：易受感染
- 感染者I：易感染，且可感染别人
- 移除者R：曾被感染，但不会感染别人
接触与移出：
- 感染

Ross 疟疾传播模型¶

1.模型假设¶

某一区域内人的数量H与蚊子的数量V保持不变
记t时刻人群中易感者和感染值的数量分别为 $S_h(t)$

Lotka-Volterra模型¶

数学规划¶

运筹学¶

#### 1.分支 - 数学规划 - 线性规划 - 非线性规划 - 整数规划 - 多目标规划 - 组合优化 - 随机运筹 - 排队论 - 库存论 - 可靠性理论 - 博弈论与决策理论 #### 研究内容 - 优化理论 - 应用问题 - 实际案例

食谱问题¶

下料问题¶

0-1变量的使用 - 决策变量 - $x_{ji}$ ：第j种钢管截取的第i种短管数量

约束条件
$\sum \limits_{i= 1}^{k} x_{ji}w_i \leq W$
$\sum \limits_{i= 1}^{n} x_{ji} \geq b_i$

选址问题 -- 二维情形¶

思想：将二次约束变为一次约束

常用的一些处理¶

0-1变量的使用设 $x_i = j \Rightarrow x_{ij} = \left\{ \begin{aligned} 1, &\quad x_i = j \\ 0, &\quad x_i \neq j \end{aligned} \right.$

累计的处理： $\sum\limits_{i = 1}^{m}\sum\limits_{j = 1}^{n} jx_{ij}$

赛程编制¶

支持向量机SVM¶

超平面： $\mathbf{w\cdot x} + b = 0$ ¶

距离： $\frac{|\mathbf{w\cdot x} + b|}{||\mathbf{w}||}$

线性规划求解¶

线性规划的矩阵形式¶

目标函数： $min\quad \mathbf{c^Tx}$
约束条件： $\mathbf{Ax} = \mathbf{b}$
非负约束： $\mathbf{x} \geq 0$

标准型：¶

目标函数：极小化
约束条件：等式约束
非负约束： $\mathbf{x} \geq 0$
等式约束右端均为非负常数

整数线性规划 -- 分枝定界法（以最小值为例）¶

不断拆分区域，直到线性规划的最优解在整数处解得（如果我们不断拆分，最后一定会把整个区域分成一个个整数点）

分枝：以非整数解为基础将区域划分
定解：对于每块区域，求它的非整数型规划
剪枝：去掉不可能为最优解的区域（最小值比已有整数解处的要大）和LP的解为整数的情况

多目标规划¶

解的类型¶

绝对最优解（不一定存在）
- 在所有方面都是最好的
Pareto最优解
- 找不到每一个方面都比它好的解（即在某一方面时最好的（且不是并列的））
弱Pareto最优解（不常用）
- 找不到每一个方面都严格比他好的解（即在某一方面时最好的（可以并列））

求解¶

线性加权和法

将多目标规划转化为单目标规划，计算 $min \sum \limits_{k=1}^{p}\lambda _kf_k(x)$
- 求得结果为Pareto最优解
主要目标法

将多目标规划转化为单目标规划，计算 $min \ f_k(x)，满足f_i(x)<u_i(i\neq k$
- 求得结果为弱Pareto最优解
理想点法
分层排序法

在最重要的目标上求最优解，然后在次重要的目标上求最优解，以此类推
- 求得结果为Pareto最优解

投资组合问题¶

如何使收益最大，风险最小？

Info

如何使收益最大，风险最小？

定义¶

风险：投资组合的收益率的方差

组合优化¶

从离散的对象集合中选取一个或多个对象，使得满足一定的约束条件，使得某种指标达到最优

P问题与NP问题¶

P问题¶

有（确定性）多项式时间内算法的问题

NP问题¶

有非确定性多项式时间内算法的问题
证明：多项式时间内可验证某个解是不是最优解（现实中不存在）
一个例子：Hamilton回路

是否存在一条路径，经过每个顶点一次且仅一次

对于这个问题，我们可以很容易地验证一个解是否是满足条件，但是我们却很难找到这样的解

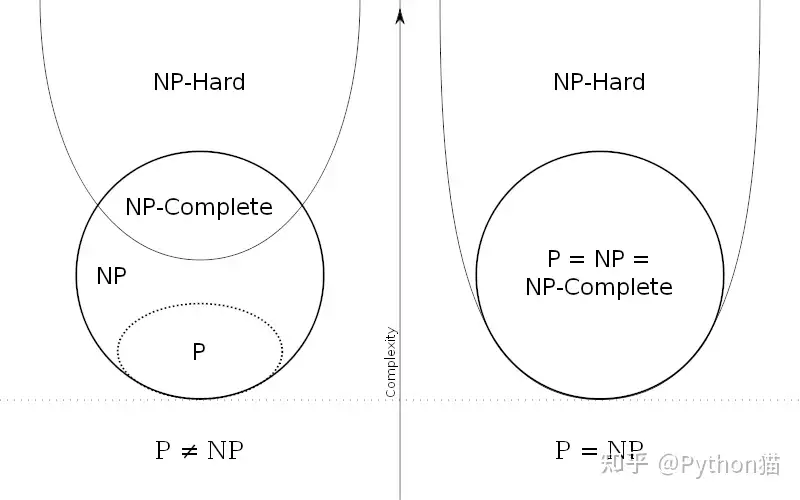
NP完全问题¶

定义
- 一个问题是NP问题
- 所有NP问题都可以归约为它（解决了它，就能以多项式时间解决所有NP问题）

NP-Hard问题¶

定义
- 所有NP问题都可以归约为它（不一定是NP问题）

P和NP问题

贪心¶

每一步都选择当前最优的可行解，但最终得到的结果不一定是最优解，需要额外证明

场馆安排问题¶

以结束时间从小到大的顺序排序

动态规划问题¶

启发式算法¶

近似算法¶

图论¶

概念¶

迹：经过边不相同的途径
路：经过顶点不相同的途径
- $路\in迹$
二部图：顶点可分为两个集合，每条边的两个顶点分别属于不同的集合
- G为二部图的充要条件：G中不含奇数环（奇数条边构成的环）
子图
- 生成子图：删去一些边
- 导出子图：删去一些点，以及与这些点相关的边

最小生成树¶

Krukal算法¶

思想：从小到大加入边，若不构成环，则加入（贪心）

最短路¶

特殊顶点集¶

顶点覆盖：顶点集中的每条边至少有一个端点在集合中（可有混日子的，去掉也是独立集）
独立集：顶点集中的任意两个顶点都不相邻
支配集：顶点集中的每个顶点或者在集合中，或者与集合中的某个顶点相邻
团：团中的任意两个顶点都相邻

匹配¶

定义：图G的一个匹配是G的一个边集(边的集合)，其中任意两条边都不相邻(连在同两点上)
最大匹配：边数最多的匹配
完美匹配：所有顶点都和匹配中的某条边相关联
最大权匹配：权值和最大的匹配

选址问题¶

着色¶

图G的k着色：用k种颜色对图G的顶点进行着色，使得任意两个相邻的顶点着不同的颜色，等价于将图的顶点集划分为k个两两不相交的独立集之并
最小k值成为图的色数，记为 $\chi(G)$

网络流¶

定义¶

网络：有向图，每条边都有一个容量c(a)
流：从源点到汇点的路径，每条边的流量不超过容量
最大流：流量最大的流
割：将网络分为两个集合，源点在一个集合，汇点在另一个集合
最小割：割中流量最小的割

最小费用流¶

给定每个顶点的平衡量，给出最小费用流

最大流最小割定理¶

最大流的值等于最小割的值

黑白易位¶

- 连通的正则图（每个点只连两条边）就是一个圈¶

博弈论¶

纳什均衡¶

如何求nash均衡
最优定价映射的交点

矩阵博弈¶

要求：零和博弈

Cournot模型¶

静态博弈，两家厂商同时决策

Stackelberg模型¶

动态博弈，两家厂商依次决策

稳定婚姻问题¶

男女双方各自排名，男方优先选择，女方后选择，男方选择后，女方可以选择留在原来的对象，或者选择新的对象，直到所有人都不再变动

男士选择，女士决定¶

讨价还价¶

Contested Garment¶

CG问题的解¶

- 假想的两个（或多个）水平容器等高¶

分享部分¶

范数¶

p范数： $||x||_p = (\sum \limits_{i=1}^{n}|x_i|^p)^{\frac{1}{p}}$
无穷范数（最大）：max{|x_i|}
对偶范数： $||x||_q = (\sum \limits_{i=1}^{n}|x_i|^q)^{\frac{1}{q}},\frac{1}{p}+\frac{1}{q} =1$

凸优化¶

凸集：对于集合中任意两点，连接这两点的线段仍在集合内
凸函数：对于函数上任意两点，连接这两点的线段在函数图像上方

数学建模

目录¶

数学建模之概念¶

作业与考试¶

数学基础与数学软件¶

数学基础¶

微分方程¶

运筹学¶

数值计算、反问题（e.g方程求根、微分方程数值解、有限元）¶

随机数学模型¶

数据分析、处理（数理统计、机器学习、数据挖掘、可视化）¶

社会科学中的数学方法（多属性决策）¶

计算机应用¶

程序设计语言（C，Python）¶

综合性数学软件（Matlab,Mathematica,Maple）¶

专业性数学软件（R,LINGO,CPLEX,Gurobi,COPT）¶

秘密共享（复记本节）¶

锁与钥匙：¶

门限机制：¶

Samir门限机制(r,n)(r,n)¶

中国剩余定理¶

Asmuth-Bloom门限机制¶

PageRank（复看）¶

排序机制——网页重要度的原则与假设¶

网页重要度¶

PageRank的数学基础¶

PageRank的计算实现¶

随机浏览模型¶

马尔科夫过程¶

数论及组合数学（复记）¶

安全状态与不安全状态¶

NIM游戏与二进制¶

随机模型¶

疾病监测¶

Monty Hall问题¶

数学期望¶

赌徒破产问题¶

面试问题¶

动态规划¶

差分方程¶

种群增长模型¶

离散单种群模型¶

1.假设¶

2.增长模型¶

混沌¶

连续单种群模型¶

生物数学模型¶

传染病--SIR模型¶

1.模型假设¶

Ross 疟疾传播模型¶

1.模型假设¶

Lotka-Volterra模型¶

数学规划¶

运筹学¶

食谱问题¶

下料问题¶

选址问题 -- 二维情形¶

常用的一些处理¶

赛程编制¶

支持向量机SVM¶

超平面：\mathbf{w\cdot x} + b = 0\mathbf{w\cdot x} + b = 0¶

线性规划求解¶

线性规划的矩阵形式¶

标准型：¶

整数线性规划 -- 分枝定界法（以最小值为例）¶

多目标规划¶

解的类型¶

求解¶

投资组合问题¶

定义¶

组合优化¶

P问题与NP问题¶

P问题¶

NP问题¶

NP完全问题¶

NP-Hard问题¶

贪心¶

场馆安排问题¶

动态规划问题¶

启发式算法¶

Samir门限机制 $(r,n)$ ¶

超平面： $\mathbf{w\cdot x} + b = 0$ ¶